この記事は旧ブログからのリライトです。
義務教育では、円周率は3.14、一時期は3ということで教えています。私としては、円周率は円周率であって、どちらも厳密には不正解と考えていて、普段は便宜的に3.14で計算していたり、厳密な技術設計をするにはより精密な3.1415で計算していますが、Excelでの計算ではとても厳密な円周率を返すPI関数があるので、それをそのまま使っています。
しかし、そもそも、円周率は3.14という常識は合っているのでしょうか。
誰も疑わなかった常識をExcelで検証してみましょう。
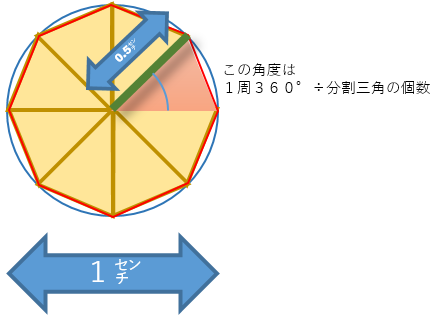
円を8個に分割した三角形で考える
次の手順でExcelで計算してみます。
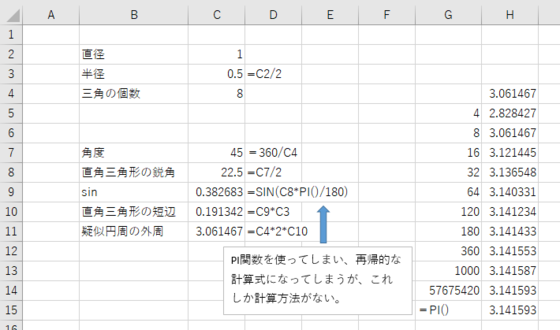
直径1cmの円周は3.1415・・・cmで半径は0.5cmです。
それを8つの二等辺三角形に分け、三角形一つ一つの短辺の合計がほぼ円周ということにします。
分割した三角形はピタゴラスの定理で計算できるように、2つに分割して直角三角形にします。
この直角三角形の鋭角は1周360°の三角形を8つに分けたものを2つに分けたので、360°÷三角形の個数÷2となります。
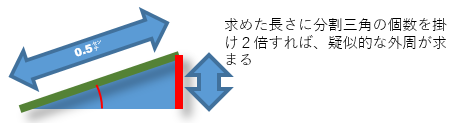
直角三角形の短辺は三角関数SINのこの角度を指定して求めた数値に半径を掛ければ求まります。
ここで問題があります。Excelで三角関数を扱うことができますが、私たちが知っている360°の角度で考えられておらず、ラジアンとして計算されます。そこで、図形学的に角度に円周率÷180の数値を掛け合わせる必要があります。ここで、円周率を使うので、円周率を求めるのに円周率を使うことになり、再帰的な計算となる問題があります。しかし、この方法でしか計算できませんので、この方法で計算を進めます。
この方法で求めた短辺に三角形の数に2つに分割した分を戻して×2とすることで、疑似的な円周を求めることができます。
Excelで数の多い証明をする
では三角形の個数が8ではなかったらどのような値になるのでしょうか。
Excelのテーブル機能で一覧計算をしてみます。
3600個ではほぼ3.1415と円周率にかなり近づきました。
分割数が多ければ高い精度の計算ができるようです。
まとめ
ここまでやってみて感じたのは、直径1の円周の長さを3ちょっとと求めた紀元前の人たちは偉大だと思いました。
この法則を今発見したらノーベル賞なんてぶっ飛ぶくらいの発見だったことでしょう。
これがあるおかげで車が何キロで走っているかのスピードメーターは動くわけですし、GPSで現在地がわかったり、発電所作った電気が各家庭に送られているのです。
今回は図形学的に円の外周を疑似的に求める手法を使ってみたのですが、たぶん、昔から使われた手法だと思います。
しかし、コンピュータやExcelなんかなかった時代では、今回のような計算がどのようにされていたのかはわかりません。
高速に大量の計算ができるので、大昔の偉大な数学者が求めた体験をいとも簡単に追体験できているんだなと今の時代に生まれたことを感謝するばかりです。
やはり円周率は3ちょっとで間違いなかったです。
数学的にはどんなに分割しても円周率にはなりません。しかし、Excelには計算精度というものあり、無限の精度で求められるわけではありません。Excelでは分割数が57675420で円周率と完全一致します。
確かこのような円周率の考え方を義務教育のうちに教えてもらったような・・・。
三角関数を教える段階で、このような思考実験、そもそも円周率は3.14でいいのか?という教育があると面白い学習ができるような気がします。
企業の新人研修でこのようなワークがあると面白いかも。
実際に円を描いて糸で長さ測るグループもいたりして、楽しいと思います。
Excelではこのように、証明することが大変なものでも、再計算や相対参照のおかげで複雑な計算を繰り返しできます。




コメント